Linear Convolution of two Discrete Sequences usng function Using MATLAB Code: With MATLAB code

In mathematics & signal processing, convolution is a mathematical method applied on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions.

The digital convolution with sample interval t = 1 is summarized as:

1. Flip (reverse) one of the digital functions.
   
   
2. Shift it along the time axis by one sample, j.
   
   
3. Multiply the corresponding values of the two digital functions.
   
   
4.  Summationof products from step 3 to get one point of the digital convolution at j.
   
   
5. Repeat steps 1-4 to obtain the digital convolution at all times, j where the digital functions overlap.

For example, let s_k = 2, -2, 1 and h_k = 1, 3, 1/2, -1. Convolution of these two discrete signals equals 2, 4, -4, 0, 2 1/2, -1


More References about Convulation:

MATLAB Code to Perform Convolution  of two Discrete Sequences using MATLAB conv() Function:

%Code Starts Here

clc;
clear all;
close all;
x1 = input('Enter First sequence x1(n)[] : ');
t1 = input('Enter Origin location Of Sequence x1 : ');
x2 = input('Enter Second sequence x2(n)[] : ');
t2 = input('Enter Origin location Of Sequence x2 : ');
l1 = length(x1); %length of sequence x1
l2 = length(x2); %length of sequence x2
ln = l1+l2-1; %length of convoluted sequence
y = conv(x1,x2); % performing convolution using conv() function
a = t1+l1-1;
t = t1:a;
subplot(3,1,1);
stem(t,x1);
xlabel('Time');
ylabel('Amplitude');
title('x1');
a = t2+l2-1;
t = t2:a;
subplot(3,1,2);
stem(t,x2);
xlabel('Time');
ylabel('Amplitude');
title('x2');
tn = t1+t2;
a = tn+ln-1;
t = tn:a;
subplot(3,1,3);
disp('Convoluted Sequence ');
disp(y); % For printing the convulated output in MATLAB command window
stem(t,y); %  For plotting the convulated output in MATLAB graph window
xlabel('Time');
ylabel('Amplitude');
title('Convoluted Sequence');

Sample Input (As it will be seen in the Command Window) :

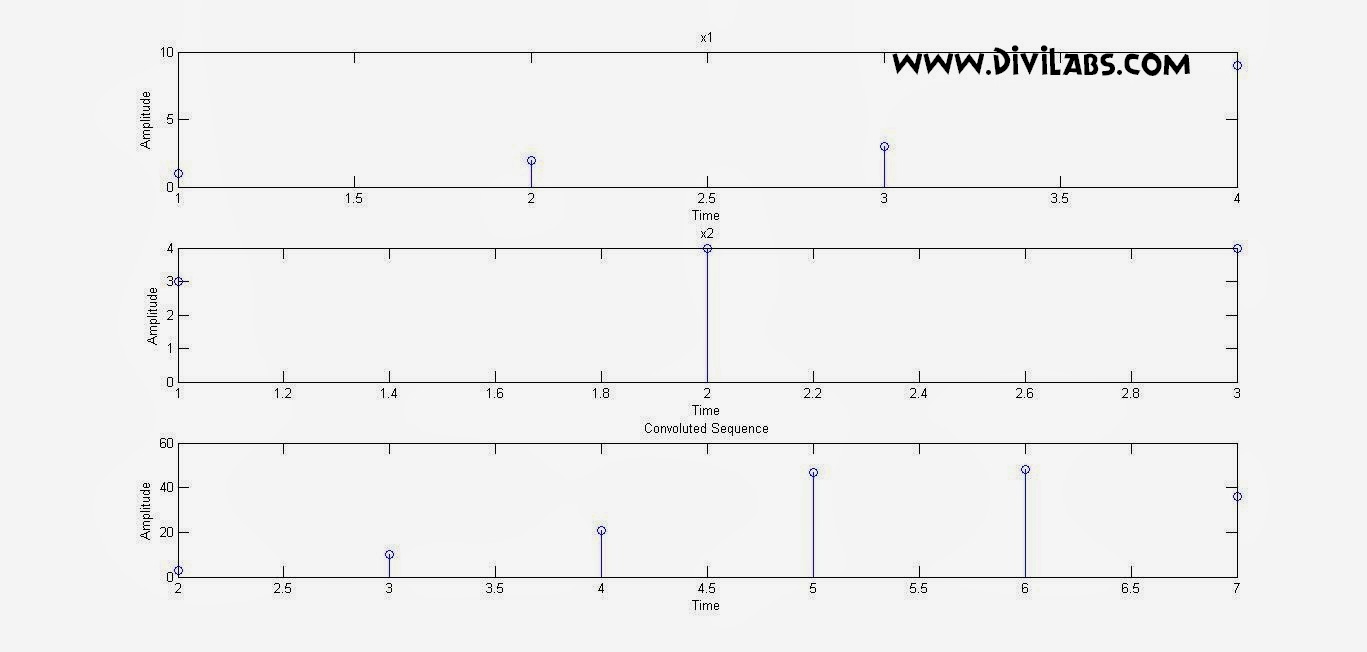
Enter First sequence x1(n)[] : [1 2 3 9]
Enter Origin location Of Sequence x1 : 1
Enter Second sequence x2(n)[] : [3 4 4]
Enter Origin location Of Sequence x2 : 1
Convoluted Sequence
     3    10    21    47    48    36

Graph Thus Obtained: (Containing the 2 input sequences along with the resulted convoluted sequences)

Visit More On Digital iVision Labs:
#FSK Simulation Code Using MATLAB
#Phase Shift Keying (PSK) Modulation MATLAB Simulation, With MATLAB Code
#Amplitude Shift Keying (ASK) Modulation MATLAB Simulation, With MATLAB Code

#Using MATLAB, Extracting individual Red, Blue & Green (RGB) planes, From a RGB Image, With Code

#Matlab Christmas Tree Plot- Christmas celebration through matlab way - Merry Christmas!

Author: Vibhutesh Kumar Singh

An active & prominent author at Digital iVision Labs! Specializing in MATLAB, C++, Arduino, OpenCV, NI Labview, Web Designing & other Electronics stuffs! Just started M.Tech. From IIIT Delhi, looking for excellent PhD Opportunities with prominent researchers. Drop a mail: vibhutesh[at]gmail.com or Follow him at....

Facebook

Twitter

Google+

Linkedin