Envelope Detection (Implementation) using Fast Fourier Transform (FFT-IFFT) (Analytic Signal)
What is an envelope?
The envelope graphically is a curve which is obtained by joining the extremities of a signal in time domain. E.g. in the figure below.
 |
| Upper Envelope of Amplitude modulated signal |
 |
| Envelope of an arbitrarily high-frequency signal (courtesy: wikipedia.org) |
Particularly the above figures represent the "peak envelope" of a signal.
In analog modulation (especially amplitude modulation) envelope detection is important since envelope of the received modulated signal is proportional to the message, which was modulated over the carrier at the transmitter end. This is done through a physical circuit consisting of a capacitor which tries follow the peaks of the input signal. Which is further smoothened through filtering.
The envelope detection can be performed using an analytical signal.
An analytic signal is a complex-valued function that has no negative frequency components. For a real-valued signal an analytic signal, consist the original function and its Hilbert transform.
i.e., e = HT(s(t)) + s(t). (HT(s(t)) is the Hilbert Transform of signal s(t)).
The basic idea of the analytical signal is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are an alias of the positive frequency components, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information but result in a complex-valued function.
For more equations and explanation involved for an analytical signal, please refer to this Wikipedia article:
https://en.wikipedia.org/wiki/Analytic_signal
The absolute value of this analytic signal in the time domain will give the envelope of the signal.
i.e., (to understand it better, convert the analytic signal to polar form),
envelope = |e|=sqrt(HT(s(t))^2 + s(t)^2)
The MATLAB implementation envelope detector according to above theory using FFT and IFFT is as follows (Code in Bold): (I have taken the example signal to be amplitude modulated signal)
An analytic signal is a complex-valued function that has no negative frequency components. For a real-valued signal an analytic signal, consist the original function and its Hilbert transform.
i.e., e = HT(s(t)) + s(t). (HT(s(t)) is the Hilbert Transform of signal s(t)).
The basic idea of the analytical signal is that the negative frequency components of the Fourier transform (or spectrum) of a real-valued function are an alias of the positive frequency components, due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded with no loss of information but result in a complex-valued function.
For more equations and explanation involved for an analytical signal, please refer to this Wikipedia article:
https://en.wikipedia.org/wiki/Analytic_signal
The absolute value of this analytic signal in the time domain will give the envelope of the signal.
i.e., (to understand it better, convert the analytic signal to polar form),
envelope = |e|=sqrt(HT(s(t))^2 + s(t)^2)
The MATLAB implementation envelope detector according to above theory using FFT and IFFT is as follows (Code in Bold): (I have taken the example signal to be amplitude modulated signal)
clc
clear
close all
Ac=2; %carrier amplitude
fc=0.5; %carrier frequency
Am=0.5; %message signal amplitude
fm=0.05; %message signal frequency
%The signal and carrier frequency is taken small for now, to make the response visible
Fs=100; %sampling rate/frequency
ka=0.5; %modulation coefficient
t=[0:0.1:100]; %defining the time range & disseminating it into samples
ct=Ac*cos(2*pi*fc*t); %defining the carrier signal wave
mt=Am*cos(2*pi*fm*t); %defining the message signal
AM=ct.*(1+ka*mt); %Amplitude Modulated wave, according to definition
plot(AM, 'b');
hold on;
N = length(AM);
X = fft(AM,N); % Find FFT of the Amplitude Modulated Signal
%Assuming there is a symmetry in spectrum we will fold and add the spectrum
%creating a new analytical signal and pad zeros to maintain N point FFT size
if(rem(N,2)==0)
envelope = ifft([zeros(1,N/2-1) X(1) 2*X(2:N/2) X(N/2+1) ],N);
else
envelope = ifft([zeros(1,(N+1)/2) X(1) 2*X(2:N/2) X((N+1)/2) ],N);
end
%we use 2*X(2:N/2) since by folding and adding through f=0 (i.e., X(1)) we
%get double the amplitude
plot(abs(envelope), 'r');
%Upper envelope
plot(-abs(envelope), 'k');
%Lower envelope
xlabel('Sample Index')
ylabel('Amplitude')
axis('tight')
hold off
Result:
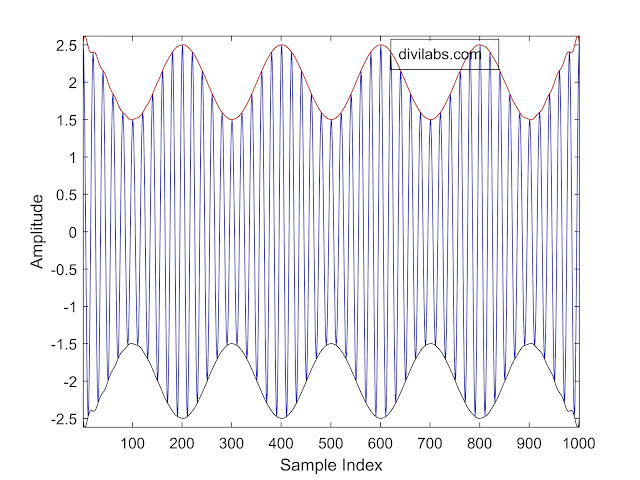 |
| Envelope detector implementation using FFT-IFFT, utilizing the concept of analytic function. |
NOTE: If the signal is having non zero mean. Then this code might not seems to work. In that case you just take the mean of the signal and subtract from the original signal and proceed with the above code.
Have you got another idea with this code or Envelope detection? You can share, in the comment section!Author: Vibhutesh Kumar Singh

0 comments: