Calculating the Global Extrema (Minima/Maxima) of a quadratic function/equation through MATLAB
An extrema is a maximum or minimum of a function. An extrema may be local (a.k.a. a relative extrema; an extrema in a given region which is not the overall maximum or minimum) or global. In this MATLAB program we are calculating the global extrema of a quadratic function/equation as entered by the user which is in the form, 'ax^2+bx+c=y'.
The program after getting the values of 'a', 'b' & 'c' from the user plots the function 'y' with the varying value of 'x'. And tells the (x,y) coordinates of the global minimum of that quadratic function.
The value of x & y are actually after taking the derivative of the function ax^2+bx+c. Refer some mathematics text in order to find more about Maxima & Minima (Extremum) Calculation.
Following MATLAB Code is for Calculating the Global Extrema (Minima/Maxima) of a quadratic function/equation.
%Global extremum of a quadratic function
%input the quadratic equation in terms of 'a','b' & 'c', ax^2+bx+c=y
a=input('Enter a for ax^2+bx+c=y:');
b=input('Enter b for ax^2+bx+c=y:');
c=input('Enter c for ax^2+bx+c=y:');
%for plotting 'y' from x=-200 to +200
xx=-100:1:100;
plot(xx,a.*xx.*xx+b.*xx+c);
title('The plot of User Entered Quadratic Equation/Function')
xlabel('x->>');
ylabel('y->>');
%min/max using first derivative
x = (-b)/(2*a);
y = ((4*a*c)-b^2)/(4*a);
disp('Coordinates of Min/max value (x,y)');
if a>0
disp('It is a minima.');
else
disp('It is a maxima.');
end
C = [x,y]
Z = b^2 - 4*a*c;% x-intercepts
A1 = (-b + sqrt(Z))/(2*a);
A2 = (-b - sqrt(Z))/(2*a);
disp('X-Intercepts:');
disp(A1)
disp(A2)
%input the quadratic equation in terms of 'a','b' & 'c', ax^2+bx+c=y
a=input('Enter a for ax^2+bx+c=y:');
b=input('Enter b for ax^2+bx+c=y:');
c=input('Enter c for ax^2+bx+c=y:');
%for plotting 'y' from x=-200 to +200
xx=-100:1:100;
plot(xx,a.*xx.*xx+b.*xx+c);
title('The plot of User Entered Quadratic Equation/Function')
xlabel('x->>');
ylabel('y->>');
%min/max using first derivative
x = (-b)/(2*a);
y = ((4*a*c)-b^2)/(4*a);
disp('Coordinates of Min/max value (x,y)');
if a>0
disp('It is a minima.');
else
disp('It is a maxima.');
end
C = [x,y]
Z = b^2 - 4*a*c;% x-intercepts
A1 = (-b + sqrt(Z))/(2*a);
A2 = (-b - sqrt(Z))/(2*a);
disp('X-Intercepts:');
disp(A1)
disp(A2)
Sample Output:
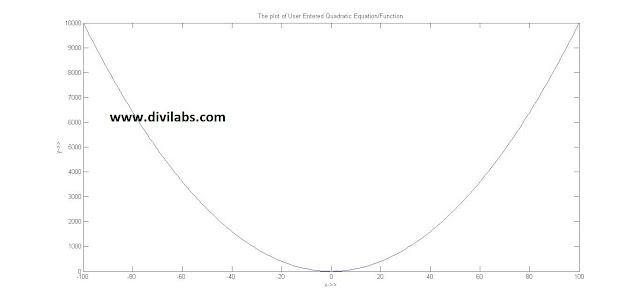
CASE 1:
 |
| Calculating the Global Extrema (Minima/Maxima) of a quadratic function/equation through MATLAB |
Enter a for ax^2+bx+c=y:1
Enter b for ax^2+bx+c=y:0
Enter c for ax^2+bx+c=y:0
Coordinates of Min/max value (x,y)
It is a minima.
C =
0 0
X-Intercepts:
0
0
Enter b for ax^2+bx+c=y:0
Enter c for ax^2+bx+c=y:0
Coordinates of Min/max value (x,y)
It is a minima.
C =
0 0
X-Intercepts:
0
0
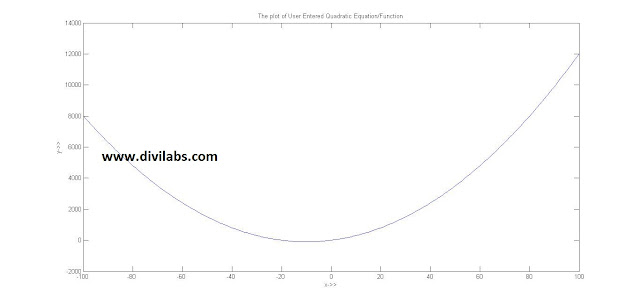
CASE2:
 |
| Calculating the Global Extrema (Minima/Maxima) of a quadratic function/equation through MATLAB |
Enter a for ax^2+bx+c=y:1
Enter b for ax^2+bx+c=y:20
Enter c for ax^2+bx+c=y:1
Coordinates of Min/max value (x,y)
It is a minima.
C =
-10 -99
X-Intercepts:
-0.0501
-19.9499
Enter b for ax^2+bx+c=y:20
Enter c for ax^2+bx+c=y:1
Coordinates of Min/max value (x,y)
It is a minima.
C =
-10 -99
X-Intercepts:
-0.0501
-19.9499

0 comments: