Digital iVision Labs!

A 2-D Median filter

The 2D median filter is a sliding-window spatial filter, it replaces the central value in the window with the median of all the pixel values lying in the window. An example of median filtering of a single 3x3 window of values is shown below.

unfiltered values

7	3	0
4	33	5
20	4	11

in ascending order they are:
0, 3, 4, 4, 5, 7, 11, 20, 33

 

After applying the median filter only '5' is preserved

*	*	*
*	5	*
*	*	*

Center value (previously 33) is replaced by the median of all nine values (5).

The median filter is also widely claimed to be 'edge-preserving' since it theoretically preserves step edges without blurring. However, in the presence of noise it does blur edges in images slightly.

How 2d median filter is applied on an Image Matrix, through a sliding window approach. Due to 2nd & 3rd condition we need to pad the edges.

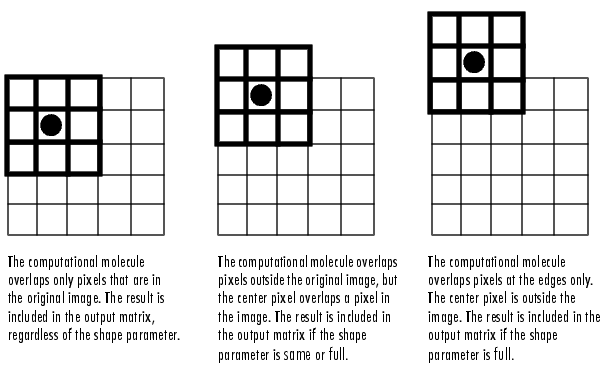(Image illustration Courtesy, CUVT Prague)

By the above illustrations, it might be clear till now how the central element of the median filter is calculated & how the sliding window approach helps to decide & replace the original valued pixel.

Also before going to the implementation of MATLAB Based Salt & Pepper Noise Removal by 2D Median Filtering without medfilt2 MATLAB Function, I suggest you to please refer the below two articles, for having a much enhanced insight of the problem.

# Adding Salt & Pepper Noise To An Image Using MATLAB : Using & Without Using IMNOISE Function 

# Padding Borders of an Image with Zeros or Any Constant Value, Using MATLAB

MATLAB Code for Salt & Pepper Noise Removal by 2D Median Filtering without medfilt2 MATLAB Function

clc
clear all
close all
i=imread('xyz.jpg'); %read the image
i=rgb2gray(i); %convert the rgb image to grayscale image
imshow(i);  %show the original image
i=imnoise(i,'salt & pepper',0.05); %add S n P noise to original image
figure,imshow(i) %show the corrupted  image
p=input('Enter the size of kernel of median filter, (n for nxn matrix):'); %specify the kernel size
pad=uint8(zeros(size(i)+2*(p-1))); %padding the zeros

%loop for padding the zeros
for x=1:size(i,1)
            for y=1:size(i,2)
                pad(x+p-1,y+p-1)=i(x,y);
            end
end 

%loop for finding the median & replacing the central pixel

 for i= 1:size(pad,1)-(p-1)
    for j=1:size(pad,2)-(p-1)
        kernel=uint8(ones((p-1)^2,1));
        t=1;
        for x=1:p-1
          for y=1:p-1
                kernel(t)=pad(i+x-1,j+y-1);
                t=t+1;
          end
        end
        filt=sort(kernel);
        out(i,j)=filt(5);
    end
 end
figure,imshow(out); %show the final recovered image

Program Execution & Results:

Original Image:

Original Image

Grayscale Version of the original image:

Grayscale Version of the original image

Image after adding the Salt & Pepper Noise

Input:
Enter the size of kernel of median filter, (n for nxn matrix):4

Resultant Noise Removed Image:

Resultant Noise Removed Image, With a kernel size 4x4

Author: Vibhutesh Kumar Singh

An active & prominent author at Digital iVision Labs! Specializing in MATLAB, C++, Arduino, OpenCV, NI Labview, Web Designing & other Electronics stuffs! Just started M.Tech. From IIIT Delhi, looking for excellent PhD Opportunities with prominent researchers. Drop a mail: vibhutesh[at]gmail.com or Follow him at....

Facebook

Twitter

Google+

Linkedin